视觉

Ransac

前言：

基于特征的图像匹配中会存在误匹配对，因此为提高匹配率，在粗匹配的基础上实现精匹配，可采用下面两种方法：RANSAC 算法和最小二乘法

一、RANSAC简介

RANSAC(RANdom SAmple Consensus随机采样一致性算法)，是在一组含有“外点”的数据中，不断迭代，最终正确估计出最优参数模型的算法。

主要解决样本中的外点问题，最多可处理50%的外点情况。
内点：符合最优参数模型的点。
外点：不符合最优参数模型的点，一般指的数据中的噪声或无效点，比如说匹配中的误匹配对和估计曲线中的离群点。
外点检测算法
应用：在计算机视觉的匹配问题中广泛应用，以寻找最佳的匹配模型，达到去除误匹配对，实现精匹配的效果。

二、RANSAC基本思想

1.步骤

1. 在样本N中随机采样K个点 	
2. 对这K个点进行模型拟合	
3. 计算其他点到该拟合模型的距离，并设置阈值，若大于阈值，为外点，则舍弃，小于阈值，为内点，统计内点个数。阈值：为经验值，由具体应用和数据集决定。
4. 然后以新的内点为基础，再次进行步骤2，得到新的拟合模型，迭代M次，选择内点数最多的模型，此时的模型为最优模型。
5. 也可以在此基础上，选择出内点数最多的模型，然后对它进行重新估计，估计的时候可以采用最小二乘法来拟合。

2.迭代次数的公式

1、n数据中内点所占的比例（内点的概率p）：

2、选取的K个点至少有一个是外点的概率：

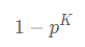
3、因此就能得到迭代M次的情况下，选取点都是外点的概率，进而得到迭代M次中，至少有一次选取点k个点都是内点的概率，也就是正确模型的概率：z一般要求满足大于95%即可。

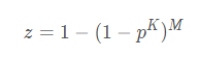
4、最终得到迭代次数M:
M = log(1-z)/log(1-p^k )

三、最小二乘法

1、最小二乘法的主要思想

通过确定未知参数（通常是一个参数矩阵），来使得真实值和预测值的误差（也称残差）平方和最小，其计算公式为

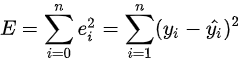
其中 yi是真实值，yi^是对应的预测值。
下图中，红色为数据点，蓝色为最小二乘法求得的最佳解，绿色即为误差

图中有四个数据点分别为：(1, 6), (2, 5), (3, 7), (4, 10)。显然，最佳解(3, 7)

四、RANSAC 与 Least Squares Fit（最小二乘法）区别

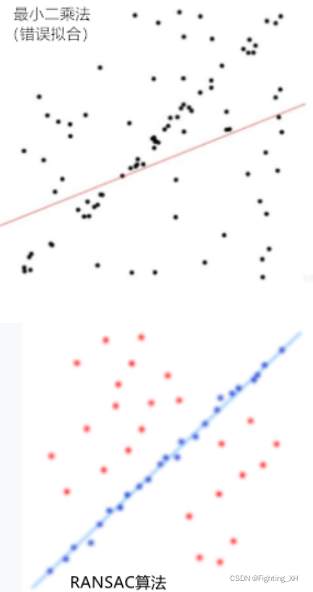
RANSAC算法：适用于含有较大的噪声或无效点的情况

最小二乘法：适用于误差比较小的情况

如下图所示，在误差比较大的情况下，肉眼也能看出拟合出的直线，但用最小二乘法拟合的直线却是错误的。而用RANSAC算法却能成功拟合。

五、RANSAC 算法的优缺点

优点：当数据中有大量的异常数据时，也能高精度的进行估计拟合。

缺点：对于异常数据超过50%的时候，拟合效果不佳。需要设置特定于问题的阈值。迭代次数若受到限制，那么达到迭代次数时拟合出来的模型可能并不是最佳模型。特定数据只能拟合出一个模型，一般多模型拟合采用霍夫变换。

六、Opencv实现RANSAC算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
//RANSAC算法
int main()
{
Mat img_object = imread("./data/101.png", IMREAD_GRAYSCALE);
Mat img_scene = imread("./data/100.png", IMREAD_GRAYSCALE);

if (img_object.empty() || img_scene.empty())
{
    cout << "Could not open or find the image!\n" << endl;
    return -1;
}
//-- Step 1: Detect the keypoints using SURF Detector, compute the descriptors
int minHessian = 800; // default: 400
Ptr<SURF> surf = SURF::create(800);
std::vector<KeyPoint> keypoints_object, keypoints_scene;
Mat descriptors_object, descriptors_scene;
surf->detectAndCompute(img_object, noArray(), keypoints_object, descriptors_object);
surf->detectAndCompute(img_scene, noArray(), keypoints_scene, descriptors_scene);

//-- Step 2: Matching descriptor vectors with a FLANN based matcher
// Since SURF is a floating-point descriptor NORM_L2 is used
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create(DescriptorMatcher::FLANNBASED);
std::vector< std::vector<DMatch> > knn_matches;
matcher->knnMatch(descriptors_object, descriptors_scene, knn_matches, 2);

//-- Filter matches using the Lowe's ratio test
const float ratio_thresh = 0.75f;
std::vector<DMatch> good_matches;
for (size_t i = 0; i < knn_matches.size(); i++)
{
    if (knn_matches[i][0].distance < ratio_thresh * knn_matches[i][1].distance)
    {
        good_matches.push_back(knn_matches[i][0]);
    }
}

//-- Draw matches
Mat img_matches;
drawMatches(img_object, keypoints_object, img_scene, keypoints_scene, good_matches, img_matches, Scalar::all(-1),
    Scalar::all(-1), std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);

//-- Localize the object
std::vector<Point2f> obj;
std::vector<Point2f> scene;

for (size_t i = 0; i < good_matches.size(); i++)
{
    //-- Get the keypoints from the good matches
    obj.push_back(keypoints_object[good_matches[i].queryIdx].pt);
    scene.push_back(keypoints_scene[good_matches[i].trainIdx].pt);
}
vector<uchar>inliers;
Mat H = findHomography(obj, scene, inliers, RANSAC);
//-- Draw matches with RANSAC
Mat img_matches_ransac;
std::vector<DMatch> good_matches_ransac;
for (size_t i = 0; i < inliers.size(); i++)
{
    if (inliers[i])
    {
        good_matches_ransac.push_back(good_matches[i]);
    }
}
drawMatches(img_object, keypoints_object, img_scene, keypoints_scene, good_matches_ransac, img_matches_ransac, Scalar::all(-1),
    Scalar::all(-1), std::vector<char>(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
namedWindow("img_matches", WINDOW_NORMAL);
imshow("img_matches", img_matches);
imwrite("img_matches.jpg", img_matches);

namedWindow("img_matches_ransac", WINDOW_NORMAL);
imshow("img_matches_ransac", img_matches_ransac);
imwrite("img_matches_ransac.jpg", img_matches_ransac);
waitKey();

return 0;
}